线程的安全问题:原子性、可见性、活跃性
前面我们了解到,多线程技术有很多好处,比如说多线程可以充分利用多核 CPU 的计算能力,那多线程难道就没有一点缺点吗?
有。
多线程很难掌握,稍不注意,就容易使程序崩溃。我们以在路上开车为例:
在一个单向行驶的道路上,每辆汽车都遵守交通规则,这时候整体通行是正常的。『单向车道』意味着『一个线程』,『多辆车』意味着『多个 job 任务』。
如果需要提升车辆的同行效率,一般的做法就是扩展车道,对应程序来说就是『加线程池』,增加线程数。这样在同一时间内,通行的车辆数远远大于单车道。
然而车道一旦多起来,『加塞』的场景就会越来越多,出现碰撞后也会影响整条马路的通行效率。这么一对比下来『多车道』就比『单车道』慢多了。
防止汽车频繁变道加塞可以在车道间增加『护栏』,那在程序的世界里该怎么做呢?
多线程遇到的问题归纳起来就三类:『线程安全问题』、『活跃性问题』、『性能问题』。
线程安全问题
有时候我们会发现,明明在单线程环境中正常运行的代码,在多线程环境中就会出现意料之外的结果,这就是大家常说的『线程不安全』。那到底什么是线程不安全呢?
原子性
举一个银行转账的例子,比如从账户 A 向账户 B 转 1000 元,那么必然包括 2 个操作:从账户 A 减去 1000 元,往账户 B 加上 1000 元,两个操作都成功才意味着一次转账最终成功。
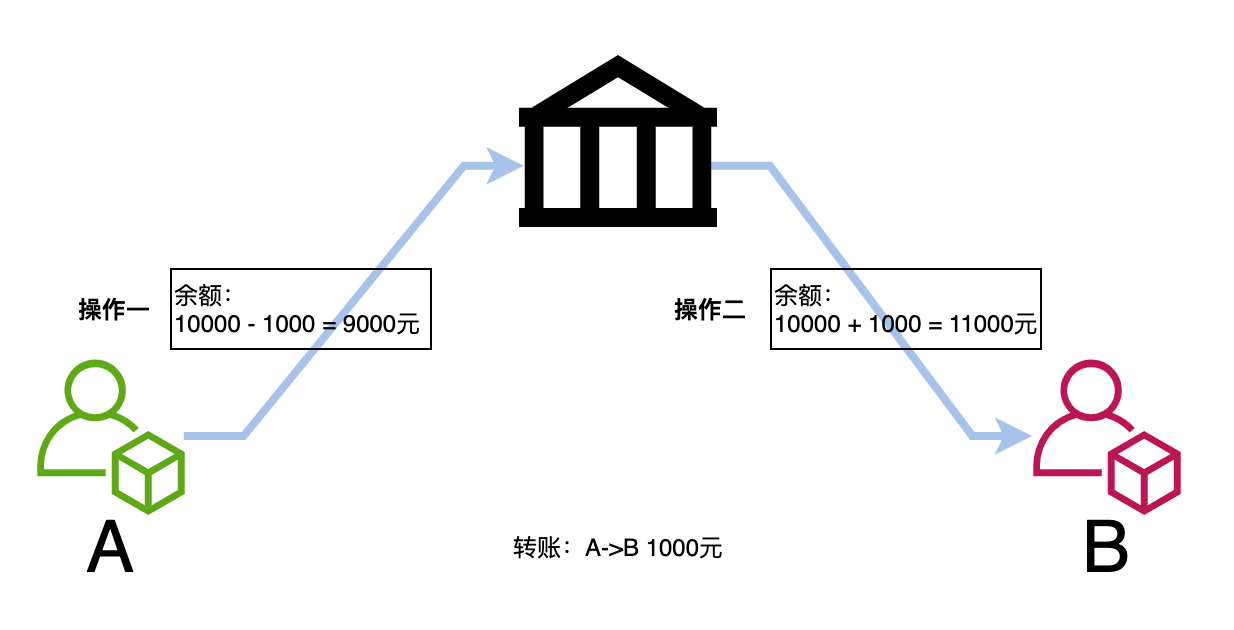
试想一下,如果这两个操作不具备原子性,从 A 的账户扣减了 1000 元之后,操作突然终止了,账户 B 没有增加 1000 元,那问题就大了。
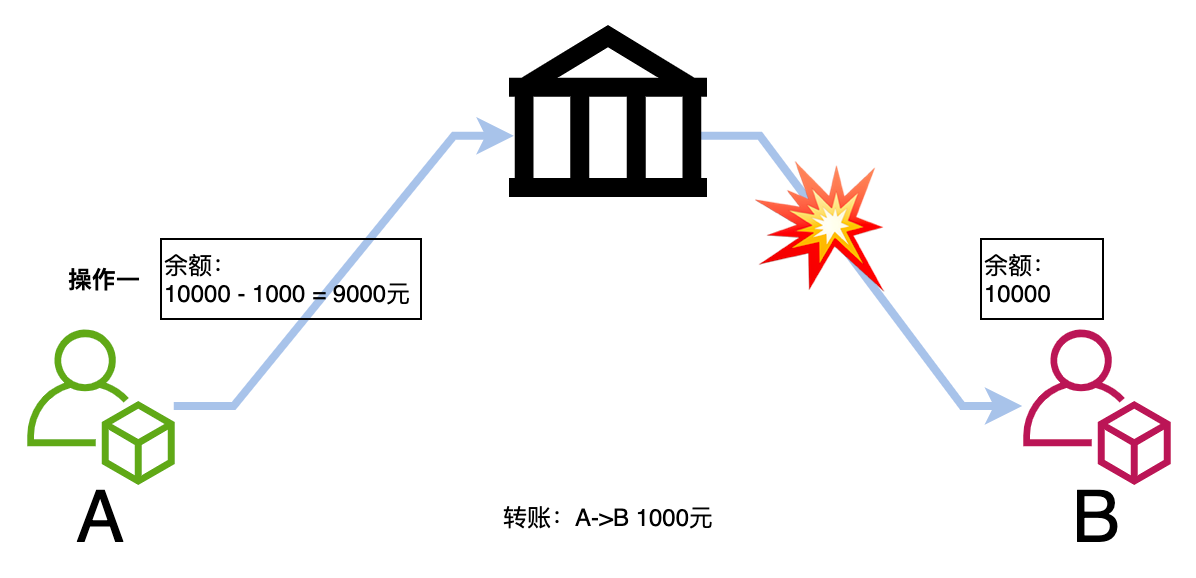
银行转账有两个步骤,出现意外后导致转账失败,说明没有原子性。
- 原子性:即一个操作或者多个操作,要么全部执行并且执行的过程不会被任何因素打断,要么就都不执行。
- 原子操作:即不会被线程调度机制打断的操作,没有上下文切换。
在并发编程中很多操作都不是原子操作,出个小题目:
int i = 0; // 操作1
i++; // 操作2
int j = i; // 操作3
i = i + 1; // 操作4上面这四个操作中哪些是原子操作,哪些不是呢?
有些小伙伴可能认为这些都是原子操作,其实只有操作 1 是原子操作。
- 操作 1:这是原子操作,因为它是一个单一的、不可分割的步骤。
- 操作 2:这不是原子操作。这实际上是一个 "read-modify-write" 操作,它包括了读取 i 的值,增加 i,然后写回 i。
- 操作 3:这是原子操作,因为它是一个单一的、不可分割的步骤。
- 操作 4:这不是原子操作。和 i++ 一样,这也是一个 "read-modify-write" 操作。
在单线程环境下上述四个操作都不会出现问题,但是在多线程环境下,如果不加锁的话,可能会得到意料之外的值。我们来测试一下,看看输出结果。
public class YuanziDeo {
private static int i = 0;
public static void main(String[] args) throws InterruptedException {
int numThreads = 2;
int numIncrementsPerThread = 100000;
Thread[] threads = new Thread[numThreads];
for (int j = 0; j < numThreads; j++) {
threads[j] = new Thread(() -> {
for (int k = 0; k < numIncrementsPerThread; k++) {
i++;
}
});
threads[j].start();
}
for (Thread thread : threads) {
thread.join();
}
System.out.println("Final value of i = " + i);
System.out.println("Expected value = " + (numThreads * numIncrementsPerThread));
}
}输出如下:
Final value of i = 102249
Expected value = 200000i 期望的值为 200000,但实际跑出来的是 102249,这证明 i++ 不是一个原子操作,对吧?
可见性
talk is cheap,show me code,来看这段代码:
class Test {
int i = 50;
int j = 0;
public void update() {
// 线程1执行
i = 100;
}
public int get() {
// 线程2执行
j = i;
return j;
}
}假如有两个线程,线程 1 执行 update 方法将 i 赋值为 100,一般情况下线程 1 会在自己的工作内存中完成赋值操作,但不会及时将新值刷新到主内存中。
这个时候线程 2 执行 get 方法,首先会从主内存中读取 i 的值,然后加载到自己的工作内存中,此时读到 i 的值仍然是 50,再将 50 赋值给 j,最后返回 j 的值就是 50 了。原本期望返回 100,结果返回 50,这就是可见性问题,线程 1 对变量 i 进行了修改,线程 2 并没有立即看到 i 的新值。
可见性:当多个线程访问同一个变量时,一个线程修改了这个变量的值,其他线程能够立即看得到修改的值。
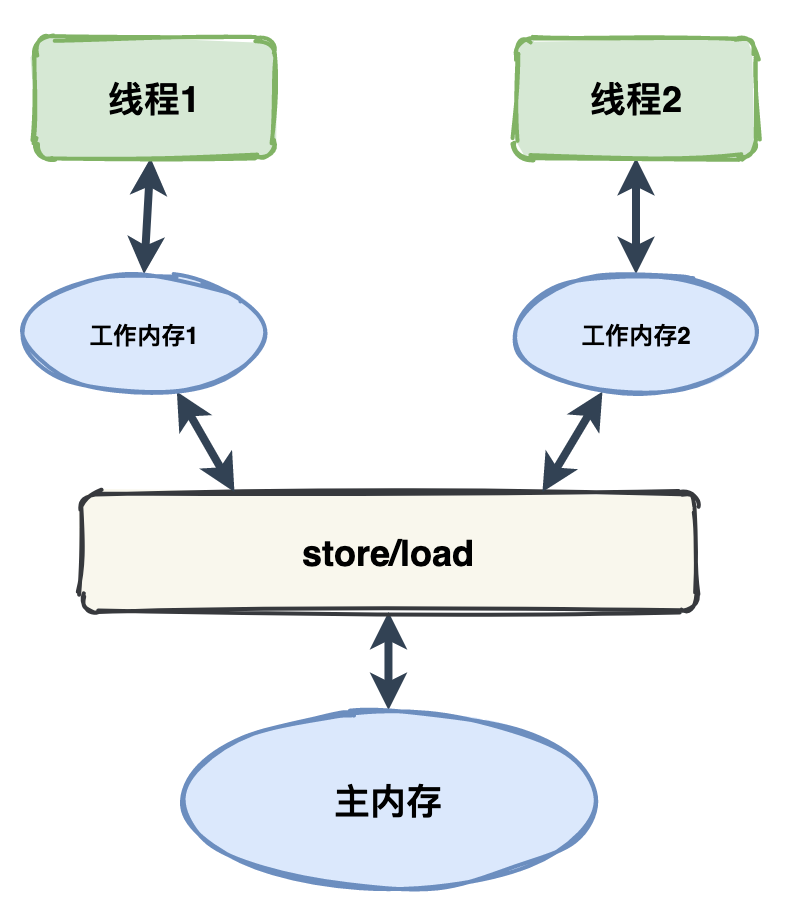
如上图,每个线程都有属于自己的工作内存,工作内存和主内存间需要通过 store 和 load 等进行交互。
为了解决多线程的可见性问题,Java 提供了volatile这个关键字。当一个共享变量被 volatile 修饰时,它会保证修改的值立即更新到主存当中,这样的话,当有其他线程需要读取时,就会从内存中读到新值。普通的共享变量不能保证可见性,因为变量被修改后什么时候刷回到主存是不确定的,因此另外一个线程读到的可能就是旧值。
当然 Java 的锁机制如 synchronized 和 lock 也是可以保证可见性的。
活跃性问题
上面讲到为了解决可见性的问题,我们可以采取加锁的方式来解决,但如果加锁使用不当也容易引入其他问题,比如『死锁』。
在讲『死锁』之前,我们需要先引入另外一个概念:活跃性问题。
活跃性是指某件正确的事情最终会发生,但当某个操作无法继续下去的时候,就会发生活跃性问题。
概念可能有点拗口,活跃性问题一般有这样几类:死锁,活锁,饥饿问题。
死锁
死锁是指多个线程因为环形等待锁的关系而永远地阻塞下去。
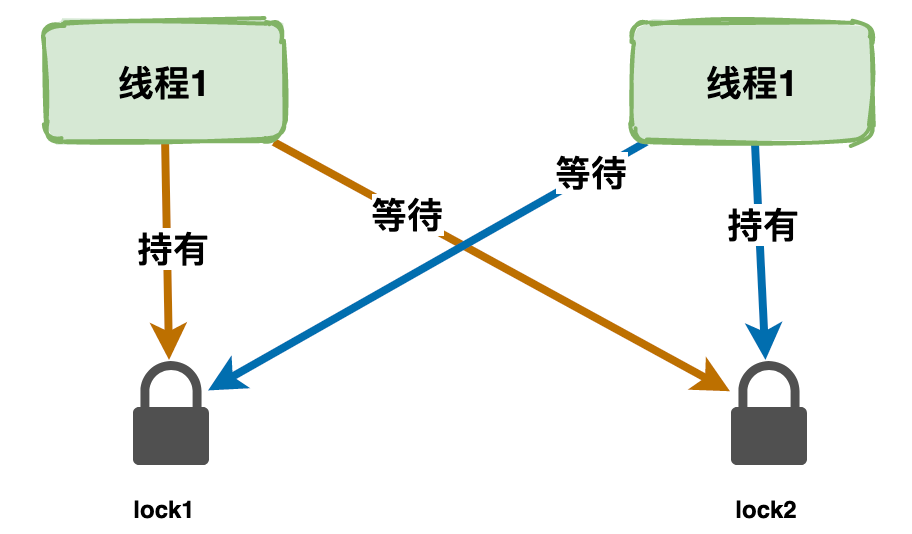
活锁
死锁是两个线程都在等待对方释放锁导致阻塞。而活锁的意思是线程没有阻塞,还活着呢。当多个线程都在运行并且都在修改各自的状态,而其他线程又依赖这个状态,就导致任何一个线程都无法继续执行,只能重复着自身的动作,于是就发生了活锁。

举一个生活中的例子,大家平时在走路的时候,迎面走来一个人,两个人互相让路,但是又同时走到了一个方向,如果一直这样重复着避让,这俩人就发生了活锁,学到了吧,嘿嘿。
饥饿
如果一个线程无其他异常却迟迟不能继续运行,那基本上是处于饥饿状态了。
常见的有几种场景:
- 高优先级的线程一直在运行消耗 CPU,所有的低优先级线程一直处于等待;
- 一些线程被永久堵塞在一个等待进入同步块的状态,而其他线程总是能在它之前持续地对该同步块进行访问;
有一个非常经典的饥饿问题就是哲学家用餐问题,如下图所示,有五个哲学家在用餐,每个人必须要同时拿两把叉子才开始就餐,如果哲学家 1 和哲学家 3 同时开始就餐,那哲学家 2、4、5 就得饿肚子等待了。
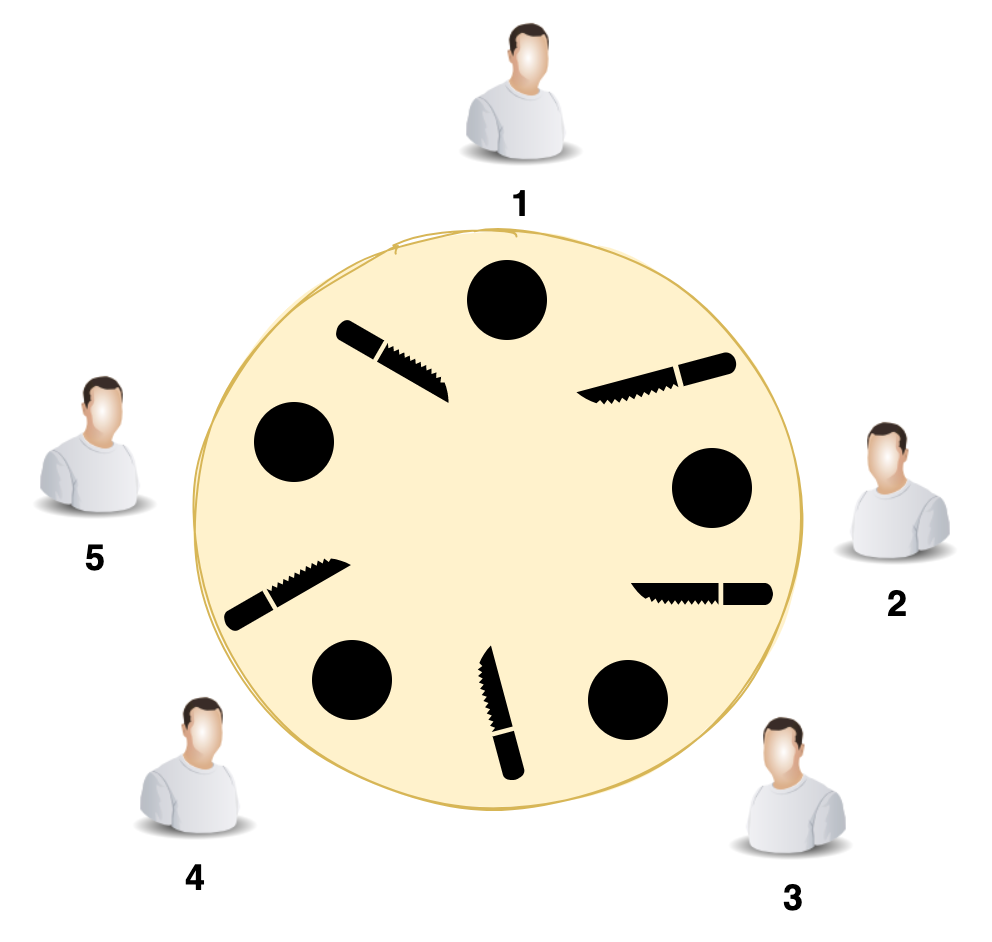
性能问题
前面讲到了线程安全和死锁、活锁这些问题,如果这些都没有发生,多线程并发一定比单线程串行执行快吗?答案是不一定,因为多线程有创建线程和线程上下文切换的开销。
创建线程是直接向系统申请资源的,对操作系统来说,创建一个线程的代价是十分昂贵的,需要给它分配内存、列入调度等。
线程创建完之后,还会遇到线程上下文切换。
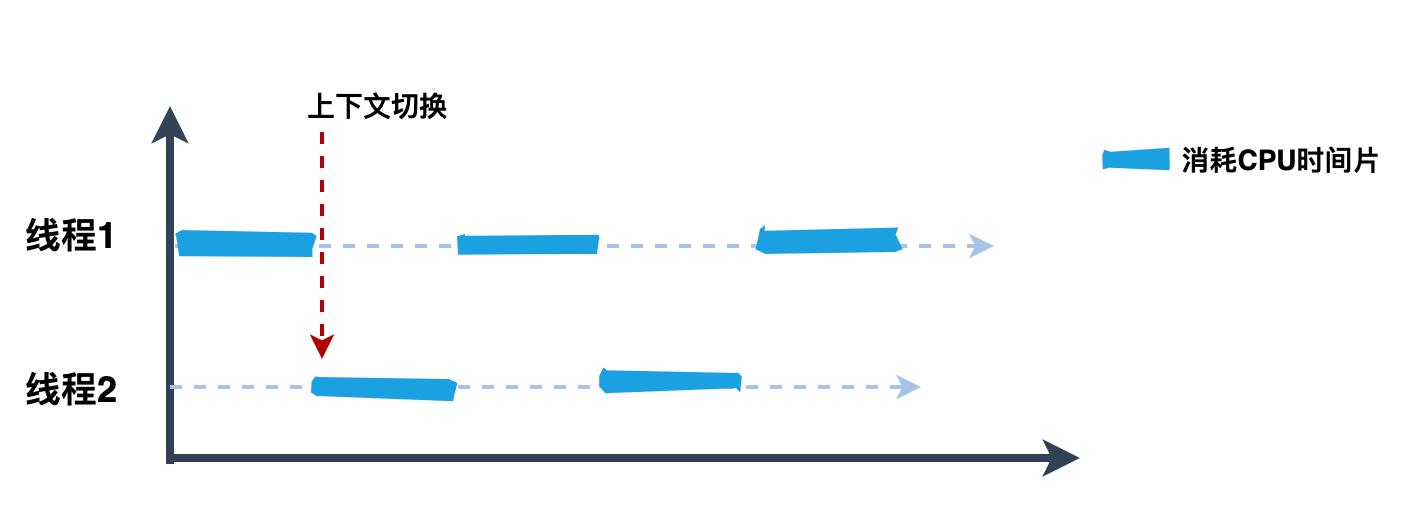
CPU 是很宝贵的资源,速度非常快,为了保证雨露均沾,通常会给不同的线程分配时间片,当 CPU 从执行一个线程切换到执行另一个线程时,CPU 需要保存当前线程的本地数据,程序指针等状态,并加载下一个要执行线程的本地数据,程序指针等,也就是『上下文切换』。
一般减少上下文切换的方法有:
- 无锁并发编程:可以参照 ConcurrentHashMap 锁分段的思想,不同的线程处理不同段的数据,这样在多线程竞争的条件下,可以减少上下文切换的时间。
- CAS 算法,利用 Atomic + CAS 算法来更新数据,采用乐观锁的方式,可以有效减少一部分不必要的锁竞争带来的上下文切换。
- 使用最少线程:避免创建不必要的线程,如果任务很少,但创建了很多的线程,这样就会造成大量的线程都处于等待状态。
- 协程:在单线程里实现多任务的调度,并在单线程里维持多个任务间的切换。
小结
多线程用好了可以让程序的效率成倍提升,用不好可能比单线程还要慢。
用一张图来总结一下上面讲的:
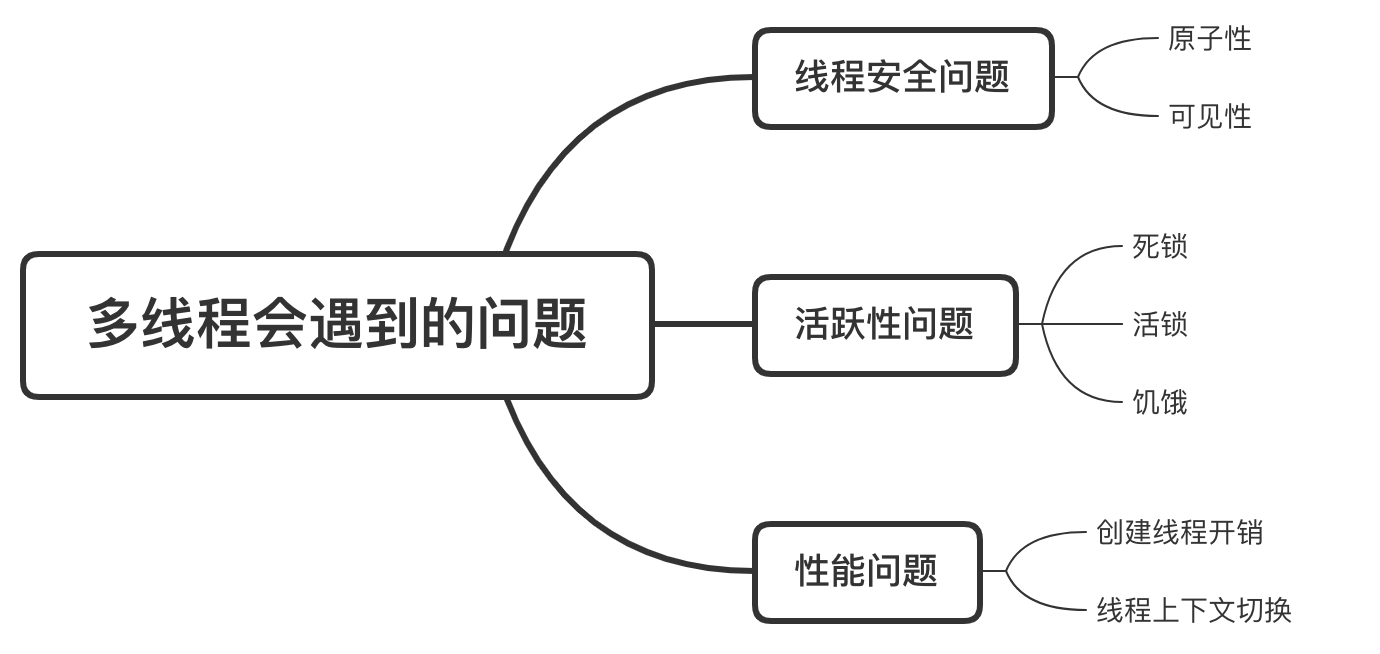
编辑:沉默王二,编辑前的内容来自于朋友雷小帅的开源仓库Java 八股文,内容很不错,强烈推荐。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第二份 PDF 《并发编程小册》终于来了!包括线程的基本概念和使用方法、Java的内存模型、sychronized、volatile、CAS、AQS、ReentrantLock、线程池、并发容器、ThreadLocal、生产者消费者模型等面试和开发必须掌握的内容,共计 15 万余字,200+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,二哥的并发编程进阶之路.pdf
加入二哥的编程星球,在星球的第二个置顶帖「知识图谱」里就可以获取 PDF 版本。